I recently came across this awesome optical illusion, first described by Stuart Anstis. Two bars, one red and one blue, move horizontally across the display. If a specific type of background texture is present, the two rectangles appear to move in anti-phase: When the red rectangle moves quickly, the blue one grinds to a halt, and vice versa. This is illusionary, of course, and the effect is gone when the background texture is removed.
The two rectangles resemble a pair of stepping (or shuffling) feet, hence the name: the stepping feet illusion. (The effect is strongest for some people if you don't look directly at the rectangles.)
The explanation for this illusion appears to be fairly straightforward (but see [1]). And, as any good illusion, it provides some insight into how our visual system works.
The crux is that the illusion will not work with just any pair of colours: There must be a luminance difference. Put differently, one stimulus must be bright (the blue rectangle in this case) and the other must be dark (the red one). In addition, there must be a comparable luminance difference in the background, which is achieved here through a pattern of alternating light and dark bands.
Now, let's say that the front and hind edges of the stimuli are on a dark band, as in a) in the figure below. In this situation, there is little contrast between the side edges of the red stimulus and the background (both are dark). Because of this, and the fact that contrast affects perceived motion, the red stimulus appears to move slowly. Conversely, there is a high contrast between the side edges of the blue stimulus (light) and the background (dark). Consequently, the blue stimulus appears to move quickly.
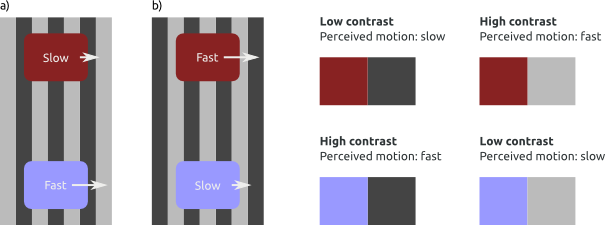
The situation reverses when the edges fall on a light band, as in b). In that case, the red stimulus appears to move faster than the blue stimulus. Taken together, this explains why the stimuli always appear to move at different speeds, and also why the speed difference alternates as the stimuli move across the display.
The cool thing is that we can derive two simple predictions from this explanation:
- If the bands are thinner, the steps should become smaller and more rapid. More shuffling-like, as it were.
- If the front and hind edges are on bands of different luminosity (which is never the case in the original illusion), there should be a caterpillar-like illusion. The stimuli should rhythmically expand, as the high-contrast front outpaces the low-contrast back, and contract, as the back catches up with the front.
To convince myself, and to show you that this indeed happens, I made a slightly warped version of the illusion. Let's call it the drunken feet illusion, or tipsy toddler. In this version of the illusion, the background becomes progressively finer. This results in a continuously morphing illusion, in which you can see both a caterpillar-like effect and a slow increase in stepping-speed.
Enjoy!
Notes
1. Howe and colleagues argue that the traditional explanation, which is the one that I discuss in this post, is inadequate. Their conclusion is based primarily on the following observation in one of their experiments: They had a stimulus move through a homogeneous pulsating background, which continuously changed in luminosity (thus modulating the contrast with the stimulus). They found that the luminosity of the background had little effect on the perceived motion of the stimulus. From this, they concluded that contrast cannot be the whole story.
Perhaps they are right, but to me their experiment is too far removed from the original illusion to allow for any strong conclusions. Therefore, I prefer to stick with the original explanation, which is simple and does a fine job.
References
Anstis, S. (2003). Moving objects appear to slow down at low contrasts. Neural Networks, 16(5-6), 933–938.
Howe, P. D. L., Thompson, P. G., Anstis, S. M., Sagreiya, H., & Livingstone, M. S. (2006). Explaining the footsteps, belly dancer, Wenceslas, and kickback illusions. Journal of Vision, 6(12). doi:10.1167/6.12.5 [Link: Open Access]



