The following illusion is a variation on the boogie-woogie illusion, described by Patrick Cavanagh and (yes, again!) Stuart Anstis. If you play the video and track the moving dot with your eyes, you will see that the edges of the diamond shape come to life. Specifically, the dots that make up the edges appear to travel along the lines. Kind of like the steps of an escalator.
So what might be going on here? I have to admit that my degree of belief in the explanation that I will outline here is modest. But that being said, here we go: Essentially, this illusion could be an instance of the aperture problem.
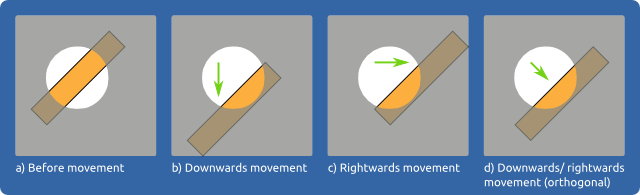
Imagine that you are looking through a hole, as in a in the figure below. Through this hole, you can see part of a bar, but not all of it. Now imagine that the bar moves, as in b, c, or d. Can you tell, based on what you can see through the hole, what the exact movement of the bar has been? No! As long as you cannot see the ends of the bar, all three forms of movement look the same.
So what do people perceive when presented with this type of ambiguous motion? Well, they tend to perceive a motion that is orthogonal to the length of the object (d). Perhaps we are biased to perceive orthogonal motion, because that's how objects generally move (do they, though?). Or perhaps it's because orthogonal motion is, in a sense, the average of all the possible motions that you could perceive. But, whatever the reason, we appear to have an innate preference for perceiving option d.
So what does the aperture problem have to do with the illusion? Where's the hole?
One way to approach this problem is by considering a single hypothetical neuron. Many neurons have a very restricted field of view. They can only 'see' a very small part of the visual field, which is called the receptive field. For our hypothetical neuron, this receptive field has been marked by the dashed circles in the figure below.
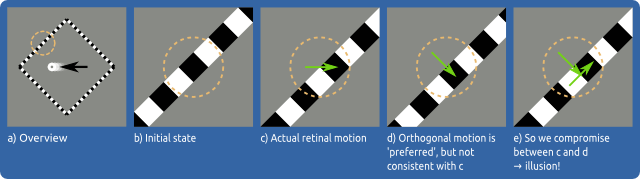
Essentially, every neuron (or at least those that cannot 'see' the corners of the diamond) is facing an aperture problem. When your eyes move to the left, the edge of the diamond moves through the receptive field of the neuron to the right (c). This is because the receptive field is tied to your point of gaze, so it moves along with your eyes (it is dragged over the edge). But this rightwards motion is not what the neuron 'likes' to see. Just as in the regular aperture problem, this neuron is biased to perceive orthogonal motion (d).
Now, if you compare the areas within the circles in c and d, you notice that they do not match. The preferred orthogonal motion is not compatible with what the neuron actually sees. This is a problem!
One way to resolve this incompatibility is to perceive the texture of the edge (the black/ white stripes) running along the length of the line (e). In other words, the combination of orthogonal motion with an escalator-like 'runny texture' is compatible with the actual visual input (c and e match up).
So quite possibly, this is why the lines of the diamond come to life: Our bias to perceive a line as moving orthogonal to its length forces us to perceive the texture of the line as moving as well.
References
Cavanagh, P., & Anstis, S. (2002). The boogie-woogie illusion. Perception, 31(8), 1005–1012.